Conclusions







Dielectric ‘Loss Factor’ (e’’) Measurement Over RF Frequencies
Between 0.1 - 40.0 GHz for Common Organic Chemicals
Between 0.1 - 40.0 GHz for Common Organic Chemicals
Abstract
Using an Agilent Network Analyzer with open ended dielectric measurement probe (85070e dielectric probe kit), the ‘loss factor’ (e’’) of common organic solvents has been measured between the range 0.1 to 40.0 GHz. Measurements were conducted in 250 mL pyrex reaction vessels filled with 125 mL of solvent with the end of the probe submersed to a depth of 5 mm. The magnitude of e’’ at the conventional microwave heating frequency 2.45 GHz is compared between solvents and to the existing data on the loss factor of water.
Keywords: Loss Factor, Dielectric Measurements, Microwave Heating, Organic Solvents.

Commercial microwave ovens operate at 2.45 GHz and are most commonly used to heat materials containing a large amount of water. Microwave heating of organic chemicals is often undertaken in commercial ovens and in this study we identify the molecular functional groups responsible for absorbing microwave energy over a spectrum of frequencies.
Microwave radiation will heat organic molecules by aligning 'molecular dipoles' with the electric field, transferring power from the radiation into the movement of the organic molecule (heat).
A molecular dipole occurs when two (or more) atoms are unevenly distributing electron density between them. The 'electronegative' atoms (increasing from N, O, F and Br, Cl, F) have a tendency to withdraw a more dense could of electrons out of a bond (pair of shared electrons) and towards its nucleus, hence ‘polarizing’ the bond.
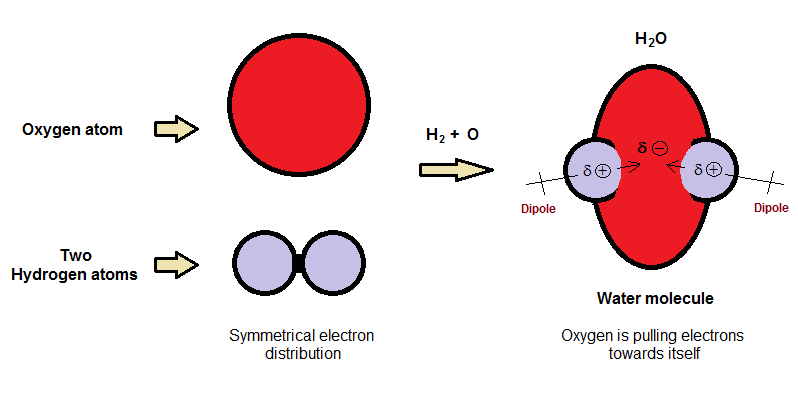
The polarization creates areas of negative (-) and positive (+) charge that has a static attraction to the electromagnetic field. Organic molecules don’t absorb electromagnetic radiation at discrete frequencies, instead a spectrum of intensities at different wavelengths occurs. Both permittivity (e’, ability of the material to be polarized and change the electromagnetic field) and loss factor (e’’, how efficiently the absorbed radiation is converted to heat) can be measured then used to calculate the angle of the molecule as it moves to align with the magnetic field (‘loss tangent’, tan d).
In this study we are only concerned with the capacity of a material to absorb radiation on a spectrum of frequencies and to use a measure of e’’ to compare with the reported values for water. Throughout the study we look at how organic chemicals absorb electromagnetic radiation over the radiofrequency (RF) spectrum (0.1-40 GHz) using a measure of loss factor (e’’).

Dielectric measurements were recorded using an Agilent Network Analyzer (E83613) with open-ended dielectric measurement probe (85070e dielectric probe kit). The measurement apparatus was set up as follows;
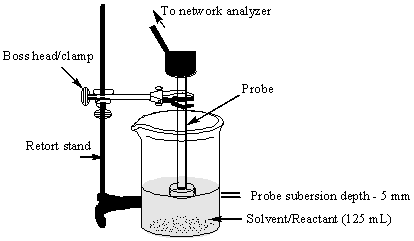

Procedure;
The tests were performed by filling the pyrex vessel (250 mL) with each organic material (125 mL) and the probe was submersed and held 5 mm below the surface of the liquid. The room temperature and solution temperature were both ~22°C .Values for e’’ were recorded over the range from 0.1 - 40 GHz, although no useful data could be collected on; Acetaldehyde (>36.20 GHz), Acetone (>37.15 GHz), Acetonitrile (>30.51 GHz) and Nitromethane (>30.51 GHz).
The tests were performed by filling the pyrex vessel (250 mL) with each organic material (125 mL) and the probe was submersed and held 5 mm below the surface of the liquid. The room temperature and solution temperature were both ~22°C .Values for e’’ were recorded over the range from 0.1 - 40 GHz, although no useful data could be collected on; Acetaldehyde (>36.20 GHz), Acetone (>37.15 GHz), Acetonitrile (>30.51 GHz) and Nitromethane (>30.51 GHz).
Analysis and Discussion;
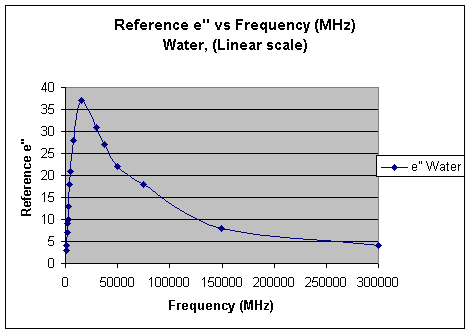
The loss factor of materials can change depending on the frequency of the incident electromagnetic radiation. This is because the interaction of the RF radiation with the dipole of a molecule will reach an optimum value at the wavelength that rotates the molecule to most efficiently generate heat (vibration). The trend in loss factor (e’’) of water at frequencies from 0.1 - 30 GHz is shown in Figure 2 (reference data recorded at 20°C)[1].
The loss factor of materials can change depending on the frequency of the incident electromagnetic radiation. This is because the interaction of the RF radiation with the dipole of a molecule will reach an optimum value at the wavelength that rotates the molecule to most efficiently generate heat (vibration). The trend in loss factor (e’’) of water at frequencies from 0.1 - 30 GHz is shown in Figure 2 (reference data recorded at 20°C)[1].

ADVERTISEMENT
Equipment
Data Acquisition and Analysis
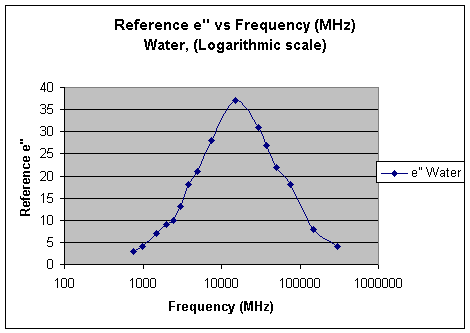
The loss factors on the RF spectrum will also change with temperature. At higher temperatures the molecules are already vibrating fast and the frequency that best absorbs RF radiation (e’’ maximum) will change depending on the existing vibration within the molecule (temperature). The loss factor for water at 22°C (our experimental temperature) and 2.45 GHz is approximately 10 although it decreases with increasing temperature as shown;
Temperature (loss factor at 2.45 GHz); 0°C (20), 20°C (11), 40°C (6), 60°C (3), 80°C (2) and 100°C (1.3).
The frequency of maximum RF absorbtion (e’’ max) increases with increasing temperature, although the magnitude of the e’’ decreases along the same trend. This means that a polar solvent, such as water, becomes ‘less polar’ with increasing temperature and more like an organic solvent. The RF frequency for maximum e’’ and reported loss factor is summarized below (Figure 3) at different temperatures[1].
Our Experimental Data: Common organic solvents (AR grade) and a number of useful reactant chemicals (LR grade) were chosen for a study on dielectric loss factor (Figure 4) to examine the effect of functional groups on dielectric heating of both the solvent and reactant at 2.45 GHz. For each chemical, the measured loss factor (e’’) at 2.45 GHz (~22°C) is tabulated in brackets.
| Approx. Temperature and e'' | Frequency/Wavelength at e'' max |
|||
| Temp (oC) | e'' (max) Water | Frequency (MHz) | Frequency (GHz) | Wavelength (cm) |
| 0 | 40 | 12492 | 12.49 | 2.4 |
| 20 | 37 | 15779 | 15.78 | 1.9 |
| 40 | 34 | 24983 | 24.98 | 1.2 |
| 60 | 30 | 44746 | 44.75 | 0.67 |
| 80 | 26 | 74950 | 74.95 | 0.4 |
| 100 | 23 | 119920 | 119.92 | 0.25 |
| Reference: Water (10) |
| Acetaldehyde (0.07) |
| n-Butylamine (transparent) |
| Cyclohexanol (0.41) |
| Diethylamine (0.01) |
| Ethanolamine (7.39) |
| Formamide (46.80) |
| Pentanedione (5.56) |
| Acetic Acid (1.35) |
| Acetonitrile (1.65) |
| Acetone (0.95) |
| Dichloromethane (DCM, 0.25) |
| Diethyleneglycol (Digol, 5.47) |
| N,N-Dimethyl Formamide (DMF, 5.90) |
| Dimethylsulfoxide (DMSO, 12.61) |
| Ethanol (7.72) |
| Diethyl Ether (0.06) |
| Ethyl Acetate (0.30) |
| Isopropanol (2.81) |
| Nitromethane (1.73) |
| Pyridine (1.19) |
| Tetrahydrofuran (THF, 0.25) |
Reactant Data
Solvent Data
Since solutions have been measured at ~22°C, the recorded data represents the initial heating capacity from room temperature. We compared the loss factor of materials at 2.45 GHz and considered materials with a loss factor of less than 1 to be mainly transparent, 1-5 is moderately absorbing and above 5 is highly absorbing (Figure 5).
| RF Transparent Materials | |
| Solvents | Reactants |
| Diethylether (0.06) | n-Butylamine (transparent) |
| THF (0.25) | Diethylamine (0.01) |
| DCM (0.25) | Acetaldehyde (0.07) |
| Ethyl Acetate (0.30) | Cyclohexanol (0.41) |
| Acetone (0.95) | |
| Moderately RF Absorbing Material | |
| Solvents | Reactants |
| Pyridine (1.19) | None |
| Acetic Acid (1.35) | |
| Acetonitrile (1.65) | |
| Nitromethane (1.73) | |
| Isopropanol (2.81) | |
| Highly Absorbing Materials | |
| Solvents | Reactants |
| Digol (5.47) | Pentanedione (5.56) |
| DMF (5.90) | Ethanolamine (7.39) |
| Ethanol (7.72) | Formamide (46.80) |
| DMSO (12.61) | |

ADVERTISEMENT

Microwave RF transparent chemicals
At 2.45 GHz, solvents containing the ‘Ether’ functional group (Diethylether and THF) were almost microwave transparent, as was the ‘Chlorinated Hydrocarbon’ DCM and ‘Ester’ (Ethyl Acetate) functional groups. The primary and secondary ‘Amine’ functional groups (n-Butylamine and Diethylamine respectively) were completely transparent. The ‘Aldehyde’ functional group (acetaldehyde) contains a ‘Carbonyl’ (C=O, bond) that was transparent in acetaldehyde. The ‘Ketone’ functional group present in acetone also has a carbonyl, but showed some absorbance perhaps due to tautomeric forms of the ketone in the acetone molecule. Cyclohexanol is a secondary ‘Alcohol’ and has an O-H bond similar to water, but is attached to a cyclic hydrocarbon structure and has low absorbance.
At 2.45 GHz, solvents containing the ‘Ether’ functional group (Diethylether and THF) were almost microwave transparent, as was the ‘Chlorinated Hydrocarbon’ DCM and ‘Ester’ (Ethyl Acetate) functional groups. The primary and secondary ‘Amine’ functional groups (n-Butylamine and Diethylamine respectively) were completely transparent. The ‘Aldehyde’ functional group (acetaldehyde) contains a ‘Carbonyl’ (C=O, bond) that was transparent in acetaldehyde. The ‘Ketone’ functional group present in acetone also has a carbonyl, but showed some absorbance perhaps due to tautomeric forms of the ketone in the acetone molecule. Cyclohexanol is a secondary ‘Alcohol’ and has an O-H bond similar to water, but is attached to a cyclic hydrocarbon structure and has low absorbance.
Moderately RF absorbing chemicals
The tertiary aromatic amine (pyridine) is somewhat absorbing due to the dipole created by an electronegative nitrogen atom within the molecule. The ‘Carboxylic Acid’ functional group (acetic acid) shows only moderate absorbance at room temperature. This may be expected to change with temperature, since the molecule contains both carbonyl and O-H functionality, both of which contain electronegative oxygen atoms that create strong dipoles. The ‘Nitrile” functional group (acetonitrile) contains a polarized nitrogen-carbon triple bond and absorbs moderately. The ‘Nitro’ functional group (nitromethane) can be considered ‘ionic’ but shows only moderate absorbance. Isopropanol is a secondary alcohol (like cyclohexanol) and has an O-H group, attached to a small hydrocarbon chain. It is smaller than cyclohexanol and able to rotate in the electromagnetic field, showing a moderate absorbance that is significantly higher than the cyclohexanol.
The tertiary aromatic amine (pyridine) is somewhat absorbing due to the dipole created by an electronegative nitrogen atom within the molecule. The ‘Carboxylic Acid’ functional group (acetic acid) shows only moderate absorbance at room temperature. This may be expected to change with temperature, since the molecule contains both carbonyl and O-H functionality, both of which contain electronegative oxygen atoms that create strong dipoles. The ‘Nitrile” functional group (acetonitrile) contains a polarized nitrogen-carbon triple bond and absorbs moderately. The ‘Nitro’ functional group (nitromethane) can be considered ‘ionic’ but shows only moderate absorbance. Isopropanol is a secondary alcohol (like cyclohexanol) and has an O-H group, attached to a small hydrocarbon chain. It is smaller than cyclohexanol and able to rotate in the electromagnetic field, showing a moderate absorbance that is significantly higher than the cyclohexanol.
Highly RF absorbing chemicals
The primary alcohol group (ethanol) absorb strongly, although Digol, which has two primary alcohols on the same carbon chain as ethanol, absorbs less strongly since it is symmetrical. The tertiary ‘Formyl Amide’ group (DMF) absorbs strongly since the carbonyl is polarized by both nitrogen and oxygen. Polarization occurs to a larger extent in the ‘Sulfoxide Ether’ group (DMSO) where sulphur is polarized by three oxygen atoms, as such the solvent DMSO is highly absorbing.
The primary alcohol group (ethanol) absorb strongly, although Digol, which has two primary alcohols on the same carbon chain as ethanol, absorbs less strongly since it is symmetrical. The tertiary ‘Formyl Amide’ group (DMF) absorbs strongly since the carbonyl is polarized by both nitrogen and oxygen. Polarization occurs to a larger extent in the ‘Sulfoxide Ether’ group (DMSO) where sulphur is polarized by three oxygen atoms, as such the solvent DMSO is highly absorbing.
The reactant pentandione contains a ‘1,3-diketone’ system that exits as a tautomer to form the secondary ‘olefinic alcohol’. 1,3-Pentanedione shows higher absorbance than the ‘alkyl’ secondary alcohol (isopropanol) since the olefin contains more electrons that can be polarized. Ethanolamine contains both primary alcohol and primary amine functional groups on the same carbon chain. The primary amine group (n-Butylamine) was proven to be RF transparent and the primary alcohol group (ethanol) strongly absorbing. Having both on the same molecule led to a decrease in absorption due to an increase in symmetry between electronegative atoms, decreasing the overall strength of the dipole.
The formamide molecule is a primary ‘formyl amide’ and has both carbonyl and amine groups. It is very small and has a large dipole. The loss factor for formamide at 0.1 MHz (~19) increases with frequency and reaches ~47 at 2.45 GHz (conventional microwave heating) to a maximum of ~51.5 at 4.27 GHz. It decreases towards ~15 as frequency is increased to 40 GHz. At the conventional heating frequency (2.45 GHz), formamide absorbs five times as much microwave radiation than water and is close to the optimal frequency for dielectric loss at 22°C. In contrast, the maximum dielectric loss for water at 22°C is at a frequency of ~9.20 GHz with an e’’ value of 37, less than that of formamide at the 2.45 GHz frequency.
Conclusions
Analysis of e’’ with Frequency
The highly absorbant chemicals; formamide, DMSO and DMF, reach their loss maximum at 6.63 and 19.4 GHz respectively. They continue to absorb RF at an e’’ greater than 10 at frequencies toward 40 GHz. RF absorbing solvents commonly have a maximum dielectric loss at a specific frequency. The e’’ maximums measured were; isopropanol (7.8, 389 MHz), digol (10.4, 475 MHz), ethanol (11.0, 968.3 MHz), ethanolamine (8.9, 1.1 GHz), DMSO (21.8, 6.63 GHz), pentanedione (12.5, 8.6 MHz), DMF (22.0, 19.4 GHz). Loss factors for nitromethane and acetonitrile begin to increase above 3.3 GHz, whereas loss factors for pyridine and acetone begin to increase above 5.7 GHz. Acetaldehyde increases to a maxima at 8.1 GHz (e’’ = 3.0) and then steadily increases with frequency.
The highly absorbant chemicals; formamide, DMSO and DMF, reach their loss maximum at 6.63 and 19.4 GHz respectively. They continue to absorb RF at an e’’ greater than 10 at frequencies toward 40 GHz. RF absorbing solvents commonly have a maximum dielectric loss at a specific frequency. The e’’ maximums measured were; isopropanol (7.8, 389 MHz), digol (10.4, 475 MHz), ethanol (11.0, 968.3 MHz), ethanolamine (8.9, 1.1 GHz), DMSO (21.8, 6.63 GHz), pentanedione (12.5, 8.6 MHz), DMF (22.0, 19.4 GHz). Loss factors for nitromethane and acetonitrile begin to increase above 3.3 GHz, whereas loss factors for pyridine and acetone begin to increase above 5.7 GHz. Acetaldehyde increases to a maxima at 8.1 GHz (e’’ = 3.0) and then steadily increases with frequency.
References
[1] Approximated valued are from; M.Chaplin. London South Bank University, http://www.lsbu.ac.uk/water/microwave.html.; J. B. Hasted, Liquid water: Dielectric properties, in Water A comprehensive treatise, Vol 1, Ed. F. Franks (Plenum Press, New York, 1972) pp. 255-309.
[1] Approximated valued are from; M.Chaplin. London South Bank University, http://www.lsbu.ac.uk/water/microwave.html.; J. B. Hasted, Liquid water: Dielectric properties, in Water A comprehensive treatise, Vol 1, Ed. F. Franks (Plenum Press, New York, 1972) pp. 255-309.

ADVERTISEMENT
For graphs of dielectric measurements please refer to the web version of this page.


Frequently asked questions about plan orders, blade design, electrical work and generator matching can be found on our Q&A pages.

Continue to summaries about.....

NMR Deconstruction
Other Articles
Introduction
Figure 1. Apparatus used to measure e''
Figure 5. A categorized table of RF absorbing materials
Figure 4. Solvents & reactants
analysed at 2.45 GHz
analysed at 2.45 GHz
Figure 3. Summarized values for e''(max)
wavelengths at different temperatures[1]
wavelengths at different temperatures[1]
Figure 2. The trend of e'' vs Frequency (MHz) for water on both linear (top) and logarithmic (bottom) scales









